Why the GAIA ROSCH buoyancy power plant
(kinetic power plant) will never work

In cooperation with ROSCH holding the GAIA-Society is offering workshops in which a so-called kinetic power plant can be built up with an alleged continuous net power output of 5 – 6 kW.

However, this is physically impossible (see explanation below).

Neither is there a patent for such a type of power plant (for perpetual motion no patents are granted), nor is there a proven working prototype. Although ROSCH is claiming on its website that such a prototype had already been built in Belgrade, I could not even find the address of Rosch Tech d.o.o., Grge Andrijanovica ulica 3, br.14bc in 11000 Beograd Srbija using Google Maps.

GAIA demands for a participation in the workshop a deposit of 2,400 euros and the commitment to pay the total cost of 12,000 euros afterwards. However, these costs do not include local installation, nor inverter to connect the plant to the household wiring, nor battery, and so on.

How the system works, is only explained in a very simple manner. It is NOT explained why it is thought to function at all, since all principles of physical knowledge are contradicted.

This small website was created so that possible participants in this workshop are able to better assess risks that they incur when they get involved in this project.

The GAIA newsletter from 2014-07-28 states literally:

Their [Rosch's] buoyancy power plants are installed primarily abroad in large numbers. We met the management of Rosch AG as a competent and reputable partner. Their large project experience provides the necessary technical and economic security in order to produce small systems for our GAIA-project, that are technically sophisticated and durable.

Do you know, dear reader, only a single power plant, which was built by Rosch? I was not able to find a single one. And I am absolutely sure that such a power plant can not be found.

The detail page of the project with the name "Measurements taken" states literally:

In order to ensure correct statements regarding the power plant capacity under operating conditions, a measurement protocol of a current 12 kW prototype at ROSCH in Serbia was created. The measured values confirm that during the measurement period in the operating phase on the input side 1,8 kW were consumed while on the output side 11,37 kW were produced. A control measurement with almost the same input power resulted in 10.7 kW on the output side. Since the used generator produces 3-phase rotary current special measuring instruments were used, which have the benefits of detecting each phase separately. The system was further examined with an endoscope and the entire water column was drained in order to ensure that there is no fraud here. The measurement protocol for this prototype was already created in mid-June 2014. It does not reflect the characteristics of the mobile functional model, which was presented among other things in an easily transportable version of 2 m height at the congress in Munich.

I do not believe these statements. My physics knowledge tell a different story (see below).

However, everybody should get his/her own idea of it.

Note: Why has the following sentence been added: "It does not reflect the characteristics of the mobile functional model, which was presented among other things in an easily transportable version of 2 m height at the congress in Munich."?

Here is my short explanation of the physics behind the model.

In the featured Rosch power plant air is blown into one (or more) container at its lowest point with a compressor. The air which was blown into it forces the water out which has previously sunk downwards in the same container. This blown out water is therefore no longer located in the tank after the injection process but in the surrounding water (where else it should have gone?). If one brings 1 m³ of additional water into a certain depth, then one also has to displace 1 m³ of the surrounding water. And the energy needed for this is exactly the amount that is gained by the buoyancy. So all in all, NO EXCESS energy is gained in this process.

Explanation of the Archimedean principle

Here is the full text of my e-mail to Rosch and GAIA from 2014-08-01:

Dear Sir or Madam,

I heard about your website www.rosch.ag through the newsletter of the Association GAIA. You report about a so-called "buoyancy power plant" that does not work in my physical knowledge and understanding.

Reason: If there is air blown into a submerged tank, which is filled with water, then contained water inside the container has to be moved to the outside (i.e., into the surrounding water) which requires energy. The energy needed for this corresponds exactly to that amount of energy which can be recovered from the air-filled container through buoyancy.

In a practical application it is even necessary to put in a little more energy than can be recovered by the buoyancy force. The power plant has therefore in any case, a negative energy balance:

Energy received from the plant minus energy supplied to the plant is less than zero.

In the first place I assume that you do not act fraudulently and want to point out that any effort that is spent into planning and production of such power stations is pointless since the (3- or 4-dimensional) world in which we live in is accurately weighed and the conservation of energy is valid.

The law oft he conservation of energy states that the total energy of an isolated system (and this power plant is one of these systems) does not change with time. Energy can be converted between various forms of energy (e.g. kinetic energy into thermal energy). However, it is not possible to produce or destroy energy within a closed system.

If the output power in your power plant is actually continuously greater than the supplied energy, then it can not be a closed system. Because the energy has definitely to be supplied from somewhere. Where the energy comes from remains unanswered on your site.

Please consider the following suggestion: If you can show a working buoyancy power plant that delivers continuously more energy than it is fed, then I will withdraw my statement and have learned a lot. On your website a lot of pictures can be seen allegedly showing a working power plant. However, I think these images are without any significance similar to an advertising leaflet.

In order to facilitate things a bit: You do not even need to show a functioning power plant to me. It is sufficient if you can prove using physical arguments that the power plant permanently produces significantly more energy than it needs to be supplied. Here, however, I am very sure that you can not do that.

I already wrote the GAIA association a mail 2 days ago, in which I warned that people buy a pig in a poke when they make payments on a small power plant for a detached house, but received no answer until the present time. I want to protect these people to not invest their money in something that does not work with probability bordering on certainty.

A reputable company would explain the fundamental principle where the permanently produced energy comes from in a buoyancy power plant. But that is nowhere explained on your site. Nor is it shown where a functioning system can be viewed that produces continuously more energy as is supplied. Also I nowhere found a granted patent for a buoyancy power plant. Is there any patent at all?

As long as these questions are not clarified, I highly discourage anyone ever to put a penny into a cooperation of any kind with your company.

The answer from Rosch returned promptly – less than 2 hours later on a Friday afternoon. Namely, from the Legal Department:

Dear Mr. Suess,

we hereby make reference to your sent letter. First of all we would like to make it clear that the erroneous accuse of a crime (a fraud is such a crime) constitutes a separate offense, as well as the coercion with which you are trying to force us to disclose our trade secrets.

Since we consider your letter as enthusiastic overreaction, we do not take legal action for the moment.

Your somewhat confused legal opinion that we need to prove the functioning principle to you or how a reputable company should work in your eyes, we leave up to you. We do not want to share or even discuss with you our corporate decisions and strategies.

In addition, we have neither the time nor feel the inclination to provide tutoring.

Our Technology has been tested and confirmed at the functioning of various renowned testing and project engineering companies. There are several professional evaluation reports that we make available to business partners after providing a positive credit certificate.

Shortly to your fundamental error: our power plant is not a closed system, which physicists, which are worthy to be named as such, recognized immediately.

By careful studying our website, you could on the one hand have found the location of the functioning power plant, on the other hand also a video of it being in operation.

Yours sincerely
Klaus-Peter Gerharz
General Counsel

SaveThePlanet AG
Holding company of Rosch Group
Einfangstrasse 14

Here is my immediate answer, sent an hour later to Rosch and GAIA:

Dear Mr. Gerharz,

You really let the cat out of the bag quickly! She wears a necklace with her name on it: intimidation.

I would now like to clarify something on my behalf. I have not accused your business of fraud. A fraud needs an intention to cheat to be present. Whether there is such an intention, I do not know. I wrote literally, " In the first place I assume that you do not act fraudulently ..." This is a clear statement and no accusation. I believe it is possible that you are yourself convinced that the plant works. And I'm just convinced of the opposite. What furthermore surely is not bad ...

"My somewhat confused legal opinion" is not that you need to prove anything to me. You have to do nothing at all.

By your reaction, however, is much clearer how you act. Critics are tried to be intimidated at once. Only somebody who has to hide something responds like this. Someone who is confident in himself that he had solved the biggest problem of mankind (apart from the general problem stupidity), namely the energy problem, should act a bit more relaxed ...

Well, your technology has been "tested and confirmed by various renowned testing and engineering companies". But the "professional reports" you're hiding. It really tears me off the stool. That should attract masses of potential business partners already!! A company has solved the energy problem of humanity, put all the physics upside down and hides anything that might even prove that this is actually true. Very believable!!

The video of the demonstration power plant in Belgrade is no evidence.

Is there a granted patent for your power plant? This question you have still not answered. But it is either not necessary. Because no answer is also an answer ... and trade secrets you must also not disclose.

I'm really not to accuse you of any bad intention. Maybe you are just a bona fide person with little understanding of physics, which is totally convinced that ROSCH is the ultimate best company in the world. Maybe. I was interested in showing the GAIA Association what they have pulled ashore as their "business partner".

On the home page of the website of GAIA the saying goes:

What we do at GAIA: 1.) GAIA is an association which lays the foundations for a peaceful energy transition in an altruistic (opposite of selfish) manner. Our common goal is to actively explore the phenomenon of "free energy" and to develop devices that can make everyone self-sufficient. This knowledge we want to gradually put on an "open source" base accessible to all.

...

4.) GAIA projects aim to freely provide functioning technologies (as "open source") in the form of plans and workshops to its members. GAIA technologies serve as the basis on which each member can evolve independently after visiting a workshop. As with any "open source" developments firstly it always needs a functioning base available before it can be made available to the public for further developments.

Dear people at GAIA: Will you really form an "Alliance for independence!" with such a company? Have you actually seen a functioning power plant and checked if in Belgrade more energy is produced than is supplied? Finally, you write even under point 4 that "firstly it always needs a functioning base available before it can be made available to the public for further developments." Do you know the patent number for this gigantic achievement? You know, I do not care if you did it or not. But it offers a lot of people to buy a pig in a poke and earning straight from the start 2400 Euro. That is dishonest!!

Well, now a little physics. You, Mr. Gerharz, claiming that your power plant would not be a closed system. Well, that is to say it the least a somewhat strange statement. If the system is not closed, then where is the "hole" through which energy enters, which is then available as an eternal energy source??? This is probably one of your business secrets ...

Wake up, folks at GAIA! Should ROSCH really be your partner for peaceful energy transition? This company, which immediately intimidates anybody who doubts since not a tiny piece is explained so everybody can understand why one should spend 2400 euros for a pig in a poke. Is that really your partner of choice for the peaceful energy transition? And altruistic ... well, the best thing is if I say nothing to this point.

Think about it twice, what you're doing. I hope it's not too late for you. I mean this very seriously indeed, because my physics knowledge is guaranteed a little more comprehensive than that of Mr. Gerharz. And probably even more than that of most of your members ...

The ball is now with you. You have been warned, and afterwards you have no more good excuse, if the project fails.

Yes, and should I be wrong with my statement that the power plant does not work, then I'll sit down in the car, go to Switzerland and will apologize personally to you, Mr. Gerharz.

But still there is not a single running system in a private household in Austria ...

Best Regards
Wolfgang Süß
Computer services
Schramlgut 31
A 4180 Zwettl/Rodl
+43 699 11702749
wolfgang@wolfgang-suess.at

And then the next day, I made a small sketch and wrote the following mail to GAIA – still without answer to the present time (2014-08-04, 21 o’clock):

Dear people of GAIA,

I make one last attempt in order to prevent any harm to you.

My supplied sketch presents the key elements of the "lift power plant" of Rosch:

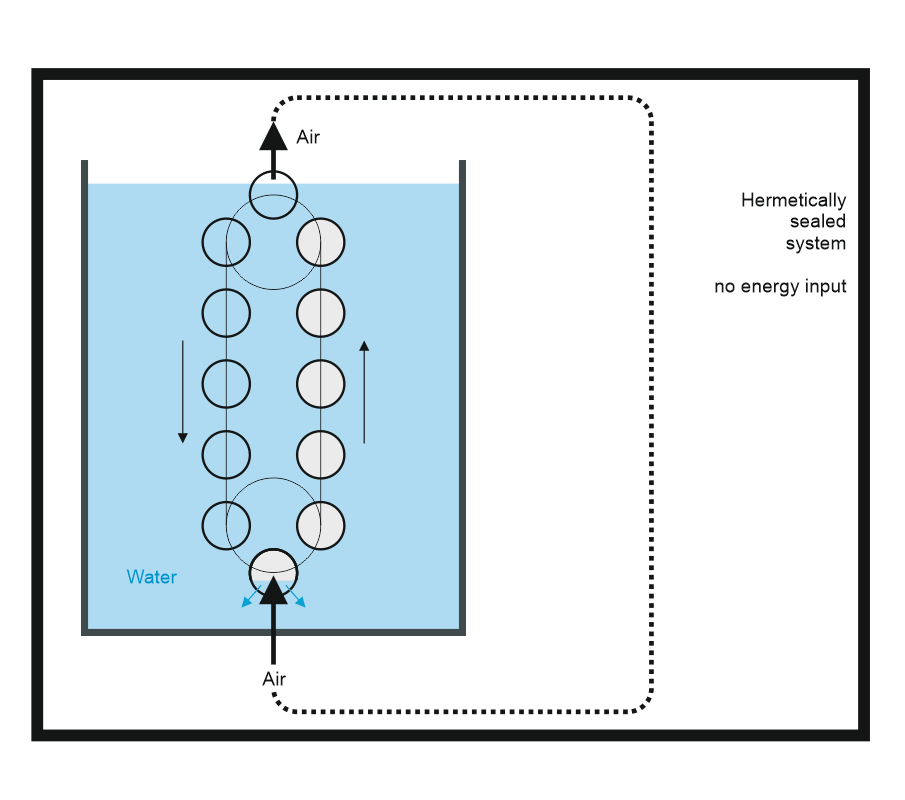
ROSCH claims (see inter alia in the mail from yesterday) that their power plant is not a closed system. But that's not true. The power plant, if it would work, it should probably also work if I close down and seal the space in which it is housed - so if I bring it in a hermetically sealed system. If I, for example, put it in a windowless basement room and lock the door, then this corresponds to such a system.

Please think about it for a little while, because your members surely do not want, that their money is "burned". And if you are unsure, then you could ask any active professor of physics, if you can extract any amount of energy from such a system in the long run. Ask a professor ... I for myself am not a professor or sworn expert. But I understood Archimedes. And I know why the conservation of energy is true.

Did you see any patent, opinions and other "evidence" of Rosch with your own eyes? Could you actually check whether the demonstration power plant in Belgrade delivers continuously more energy than was provided to it?

You ask 2400 Euro from any member who wants to set up such a plant at home already from the beginning. THIS(!) is very risky in my opinion. You are not explaining the operating principle to your members. It is not a well-known, proven system, such as a car. I do not need to know the principles of operation of a gasoline or diesel engine to drive it anyway. Since there are finally go around already millions of cars driving around every day. That is proof enough, it does not need any explanations. But something totally new, which has never happened before that contradicts the current findings of physics (conservation of energy, etc.) and to proclaim this as working perfectly and technically mature, that is negligence towards your members !!

You do not tell your members how it works. Is there someone in your association who understands how this works? Where does the energy excess come from? You write only generally speaking (quoted verbatim from your homepage):

"This technology allows you to supply your household extensively and independently with sufficient electrical energy. The system is based on using consistent physical laws and forces of nature. No perpetual motion machine but the consistent use of energy differences of two mechanical systems using available natural forces. Similarly, like a car only a startup boost is needed. After that the system is self-sufficient."

This statement is simply wrong. This system would clearly be a perpetual motion machine. Therefore, a patent for such a construction will also never ever be granted. Because the thing is not working. Ask for the patent of the company ROSCH! (I know I am repeating myself ...)

You also write on your homepage:
"Their [Rosch's] buoyancy power plants are installed primarily abroad in large numbers. We met the management of Rosch AG as a competent and reputable partner. Their large project experience provides the necessary technical and economic security in order to produce small systems for our GAIA-project, that are technically sophisticated and durable."

Soooo? Really ????? So ROSCH installed abroad in large numbers buoyancy power plants??? Have you seen EVEN ONE (apart from the times in Belgrade...)???? Where are all these many power plants? "Technically sophisticated and durable" ... that suggests that already dozens or a lot more of them were produced and are in operation. IS THIS REALLY THAT WAY?

Wake up people, yet the damage is limited. Ask yourself, get informed asking people who can judge such a thing. And please do not be so gullible, because YOU BURN MONEY OF YOUR MEMBERS!

PS: I have to date received no reply from you. Please give me feedback.

A few more notes:

In a video of GAIA, showing a prototype or a model of the lift power plant, one or more persons are to be seen, whose face was obliterated. I wonder why???

I did not succeed doing a phone call with someone from the GAIA Association. On the website there is only a postal address in Carinthia (Austria) and Germany without a contact person and also no phone number ...

The registration form for the workshop includes a wonderful last paragraph (on page 2) ...

Dear workshop participants: You are taken on a ride after all the tricks!!

2014-08-11

Addendum on 2014-08-29:

In the last newsletter GAIA cancelled the demonstration event in Belgrade because allegedly the pneumatic pump would overheat the demo power plant. I then wrote the following email (without expecting even for a second to get an answer (now I know this practice is already very good):

Dear GAIA people,

nicely and slowly your house of cards falls apart. Still you can help yourself with a few excuses and sprinkle a few words to suggest a success. "A halogen lamp with 50 W as a consumer was connected successfully." Yes, I believe you at once, that you are able to successfully connect a lamp. My grandmother could also do that.

The "specially designed diaphragm pumps" will not change anything. You will then have only one excuse less.

And finally, you wrote a very beautiful phrase: "As the capacity of the plant is directly linked to its height, we move with this 2-meter prototype on the border of the surplus energy production." So you take precautions that this prototype will not produce any surplus. It never will. An efficiency of 97% happens to be less than 1 anyway.

And if you then will have built a number of plants with a height of 5 meters, then you will notice that you come to an efficiency of 98%. Perhaps in your ranks there is also a REALLY quite stubborn guy who has a lot of money and will build a 100-meter high giant power plant ... He is then able to proudly announce to have reached an efficiency of 99%.

My percentages are naturally thumb values. But one thing I can guarantee you (!): The values are always less than 1. Energetically you have done nothing else than to bring a large flywheel running. And then it runs for a time "in standalone mode" left alone until its kinetic energy is converted into heat through friction. Then it stops and will not even wobble with one ear anymore.

Owner of this website: Wolfgang Süß, Schramlgut 31, A 4180 Zwettl an der Rodl, Phone +43 699 11702749, email: wolfgang@wolfgang-suess.at

This website uses Google Analytics, a web analysis service of Google for the statistical evaluation of visitor accesses.